Every business owner is concerned about cash flow, and the time value of money explains how you benefit from receiving cash flows quickly. You can input variables into several formulas to compute the present value and future value of payments. In addition, annuity tables allow you to calculate the value of a stream of payments.
Let’s start with a definition.
The time value of money (TVM) states that a sum of money held today is more valuable than a future payment. This money concept is true because dollars held today can be invested to earn a rate of return. The time value of money is also referred to as the net present value of money.
There’s an opportunity cost related to future cash flows. If your business receives a payment in 3 years, rather than today, you lose the opportunity to invest that money and earn a return. A future sum of money is worth less due to inflation.
Inflation is defined as the overall increase in the price of goods and services over time. Economists measure inflation by pricing a “basket” of goods and services (commonly purchased items) and monitoring how the price of the items increases each year.
As prices increase due to inflation, your purchasing power declines. Spending $100 at the grocery store buys fewer goods over time, as prices increase. Payments your business receives in the future will be less valuable, because the dollars you receive will purchase fewer goods and services.
You can compute the future value of money using a formula.
In this formula, FV is the future value of money, PV is the present value of money, and i is the interest rate. The number of compounding periods per year is given by n.
The future value of money is based on a growth rate. That rate depends on the interest rate and the period of time involved (typically a number of years).
If you change any of the variables in the time value of money formula, you’ll compute a new future value. Some formulas use payment (PMT) to indicate the dollar amount used in the formula.
Present value is the valuation of a particular cash flow today. To use the time value of money formula, let’s assume you have a $5,000 customer payment in your bank account.
FV is the value of the $5,000 payment at a future time, given your assumptions about the investment’s interest rate earned and time period.
This variable is the number of compounding periods assumed in the formula. When you compound interest, you reinvest your earnings. If interest is compounded annually, for example, the earnings are reinvested once a year. Compounding interest quarterly means that interest is reinvested four times a year.
When you choose the number of periods, the formula will produce continuous compounding, based on the total time period. If interest is compounded annually for 20 years, earnings are reinvested 20 times. However, if payments are for perpetuity, they continue indefinitely.
This variable is the annual interest rate assumed for financial calculations. A higher rate generates a larger future value.
This is the time period, which is most often stated in years.
You can find online calculators that use the variables listed above to compute the future value of a specific amount. You can also use Excel or financial calculators to perform this work. Use a step-by-step approach to input variables into the formula.
Using a future value calculator , the future value of $5,000 invested at a 6% interest rate, compounding annually for 10 years, is $8,954.24.
You can also use tables to compute the present value and future value of an amount.
This method takes a future payment and uses discounting to determine the future payment’s present value. Note that this present value method assumes compounding interest annually.
Assume that your business will receive a $10,000 payment 3 years from now. You assume an interest rate, also called a discount rate, of 5%.
Find the present value formula for a single sum ($10,000) for 3 years at 5%. This table reports that the present value factor is 0.864 (with rounding). The $10,000 received 3 years from now is worth ($10,000 X 0.864), or $8,640 today.
You can also take a single sum held today and use future value tables to determine the payment’s future value. This future value method also assumes compounding interest annually.
For this example, assume that you have $3,000 today and expect to earn a 7% return for 6 years. This future value table factor for 6 years at 7% is 1.5, and the future value of the $3,000 payment is $4,500.
By calculating compound interest manually, you get a better idea of how compounding increases the return on an invested amount.
Compounding interest is defined as earning “interest on interest,” and when you compound interest, your total earnings can be much higher. The number of time periods determines how much more money you earn using compounding.
Think about a bucket. You can envision more money going into the bucket next year if you leave your earnings in the bucket. If you took each year’s interest out, you’d only invest the original amount each year, and you’d end up with far less money over time.
These concepts apply to funding a savings account, investing in real estate, or planning for retirement.
Here’s a simple example to understand the math behind compounding interest. Assume that you invest $1,000 at a 5% interest rate in year one, which generates annual interest of $50.
In year two, you keep the original $1,000 invested, plus the year one earnings of $50. The total amount invested in year two is $1,050—which, invested at 5%, produces $52.50 in interest. By investing year one earnings of $50, you earn $52.50 in year two.
Here are the earnings for the first three years:
As the number of periods increases, the additional amount of money you earn from compounding also increases. You earn an extra $2.50 in year two, and the year three earnings are $5.13 greater than year one.
The manual calculation gives you the same result (with rounding) as the future value tables:
The calculations discussed so far assume a single amount. Annuities, on the other hand, use a series of payments.
In finance, an ordinary annuity is a series of equal payments made in consecutive periods. There are several ways to calculate an annuity payment.
The examples below assume an ordinary annuity structure.
Assume that you lease a warehouse to another business, and the lessee agrees to pay you $4,000 a year for 6 years. You decide to use a 5% interest rate to discount the payments, based on current interest rates. This table lists an annuity factor of 5.076, and the present value of the annuity is $20,304.
Your firm decides to invest $10,000 a year into a joint venture, and you expect to earn an 8% return for 10 years. The future value table provides a 14.49 factor, and the future value of the payments is $144,900.
The time of money concepts have a big impact on your company’s cash flow. If you understand the concepts and apply them, you’ll be able to make better decisions.
When you collect cash faster, you have more cash to purchase inventory, pay for marketing costs, and cover payroll expenses. A larger cash balance also gives you flexibility. If you see an opportunity to start a new product line or purchase a competitor’s business, you’ll have the cash to finance the transaction.
Here are some strategies to increase cash collections.
When you receive an invoice from a vendor, think carefully about the due date for the payment. The goal is to pay the invoice on time, but not immediately. If an invoice is due in 30 days, don’t pay the vendor tomorrow. This approach helps you conserve cash and avoid late payments that frustrate your vendors.
Accounts receivable transactions are posted when you sell goods to customers on credit and you need to monitor the receivable balance. The accounts receivable turnover ratio compares sales to accounts receivable, and your goal is to maximize credit sales while controlling the growth of accounts receivable.
You can also monitor accounts receivable using days sales outstanding (DSO). The metric calculates the average number of days it takes to collect a payment after a credit sale. A lower DSO means that you’re collecting balances faster.
Finally, offer a discount to customers who pay within 10 days, or some other time period you select. For example, offer a 2% discount for orders paid within 5 days. You’ll receive slightly less cash, but you’ll collect cash faster, which reduces the need to borrow money to fund operations.
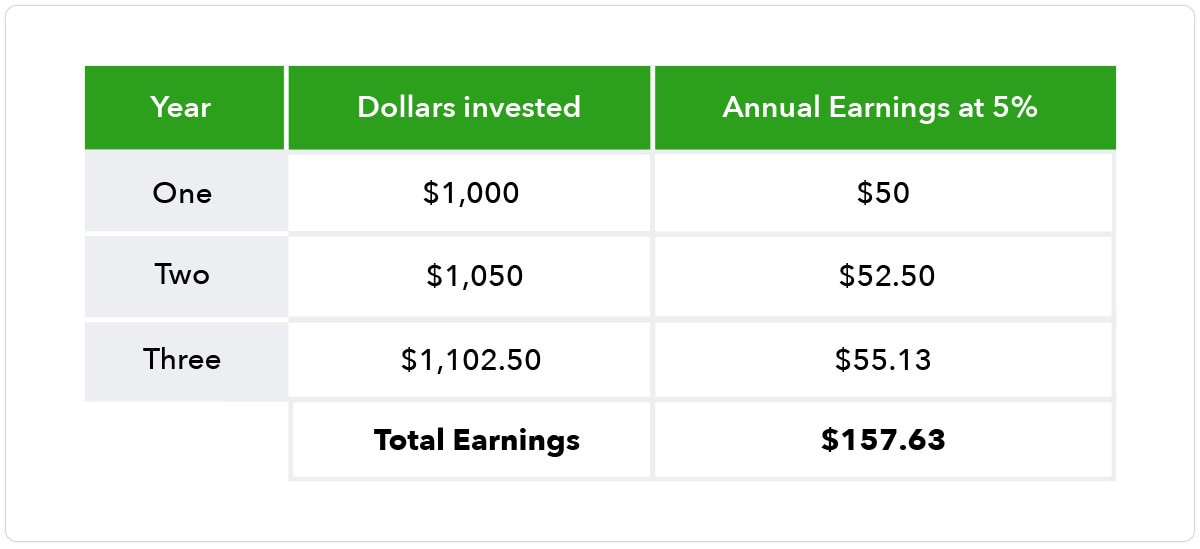
Accounting for the time value of money involves your cash and accounts receivable balances.
The present value or future value of a particular payment (or series of payments) is not reflected in your financial statements. Instead, these concepts are used to make estimates and increase your cash inflows. Use these topics to make more informed business decisions.
Call Sales: 1-877-683-3280
